排队系统的结构与量化
一个排队系统主要由两个部分组成:
- Server: 用来处理顾客的请求.
- Queue: 如果Server被占用, 那么顾客需要在Queue中进行排队.
对于一个排队系统来说, 在时刻$t$, 有如下的几个量需要关注:
- $p_n(t)$: 在时刻$t$, 排队系统中有$n$个人的概率.
- $\lambda_n(t)$: 在时刻$t$, 排队系统中有$n$个人的情况下, 单位时间内会来多少份顾客, $\frac{1}{\lambda_n(t)}$就是在时刻$t$, 两个相邻顾客到达的时间间隔.
- $\mu_n(t)$: 在时刻$t$, 排队系统中有$n$个人的情况下, 单位时间内会走多少份顾客, 这个也是Server的处理速率.
Markov排队系统
如果当$t$趋于正无穷时, 如果这个排队系统中的人数会趋于一个定值, 那么这个排队系统就会达到一个稳态, 这时, 这个排队系统就可以使用Markov链进行分析.
因为当$t \rightarrow +\infin$时, 系统趋于稳态, 因此:
- $\lim\limits_{t \rightarrow +\infin} p_n(t) = p_n$
- $\lim\limits_{t \rightarrow +\infin} \lambda_n(t) = \lambda_n$, 其中, 这个$\lambda_n$并不代表$\lambda$是$n$的函数, 而是表示当排队系统的稳态是$n$的这种情况下的$\lambda$值, 一般来说$\lambda_i$都是相等的, 相等的这个值表示平均的来客率.
- $\lim\limits_{t \rightarrow +\infin} \mu_n(t) = \mu_n$
排队系统达到稳态, 更深层次的理解是排队系统的稳态转移达到了一种动态平衡, 一种状态不会随便迁移到另一种状态, 这种现象可以用Markov链建模:

由于系统趋于稳态, 因此对于任何一个状态$n$而言, 进入系统的顾客等于离开系统的顾客, 因此:
对于状态0 : $p_0\lambda_0 = p_1\mu_1$, 那么就有: $p_1 = \frac{\lambda_0}{\mu_1}p_0$.
对于状态1: $p_0\lambda_0 + p_2\mu_2 = p_1\mu_1 + p_1\lambda_1$, 因为$p_0\lambda_0 = p_1\mu_1$, 因此$p_2 = \frac{\lambda_1}{\mu_2}p_1 = \frac{\lambda_1 \lambda_0}{\mu_2 \mu_1}p_0$
那么对于任意的状态$n$, 就有:
因此, 任意一个$p_i$都可以用$p_0$进行表示.
又由于: $p_0 + p_1 + … + p_n = 1$, 可以求出$p_0$.
求出$p_0$之后, 任意一个$p_i$就可以表示为$\lambda_i$与$\mu_i$的表达式.
因此, 如果一个排队系统可以趋于稳态, 那么根据Markov链的性质, 系统中有$n$个顾客的概率$p_n$就取决于系统的来客率$\lambda_n$以及Server的处理速度$\mu_n$.
Little定理
对于一个达到稳态的排队系统, 假设最终排队系统中的人数是$n$, 那么有: $n = \lambda_nT$.
- 其中$T$表示每一个顾客的平均等待时间.
因此, 对于一个达到稳态的排队系统, 借助Little定理, 我们还可以分析出每一个顾客的平均等待时间.
Little定理的证明
观察如下图:
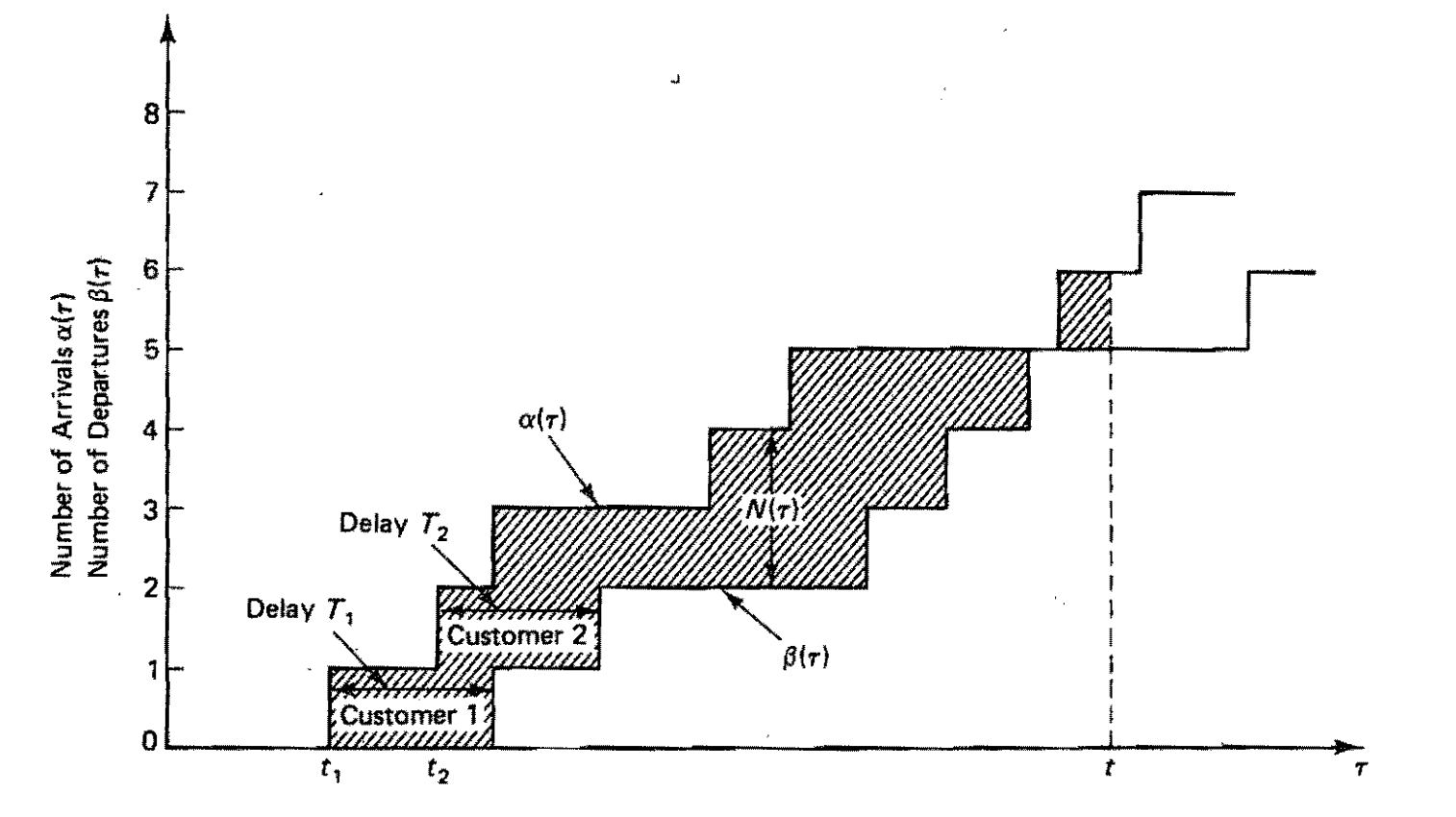
假设我的排队系统在时刻0中, 总人数是0, 也就是$N(0) = 0$.
在这个图中:
- 上面的折线代表$\alpha(t)$, 也就是在$[0, t]$内总共有多少人来我的系统中排队.
- 下面的折现代表$\beta(t)$, 也就是在$[0, t]$内总共有多少人离开了我的系统.
那么在时刻$t$, 我的排队系统中的总人数就是$N(t) = \alpha(t) - \beta(t)$.
中间部分的阴影面积可以表示为: $\int_{0}^{t}N(\tau)d\tau$, 也可以表示为$\sum_{i=1}^{\alpha(t)}T_i$, 其中$T_i$表示顾客$i$的平均等待时间.
那么就有: $\frac{1}{t}\int_{0}^{t}N(\tau)d\tau = \frac{1}{t}\sum_{i=1}^{\alpha(t)}T_i = \frac{\alpha(t)}{t}\frac{\sum_{i=1}^{\alpha(t)}T_i}{\alpha(t)}$.
两边同时取$\lim\limits_{t\rightarrow +\infin}$, 就可以得到Little定理.
排队系统的表示
排队系统可以使用A/B/C/D/E/F来表示, 其中:
- A: 单位时间来的顾客数$\lambda$的分布.
- B: 单位时间走的顾客数$\mu$的分布, 也是Server的处理速率的分布.
- C: Server的个数.
- D: 排队系统中最多允许有几个顾客.
- E: 顾客源有多少个顾客, 可以是∞, 也可以有限个.
- F: 服务规则, 例如FCFS等.
M/M/1 Queueing System
M/M/1的全称是M/M/1/∞/∞/FCFS.
当系统繁忙度$\rho = \frac{\lambda}{\mu} \in (0, 1)$时, 系统会趋于稳态.
有n个顾客的概率
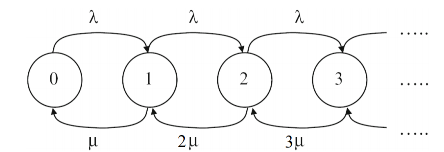
状态转移图如下:

对于状态0: $p_0 \lambda = p_1 \mu$, 那么有: $p_1 = p_0 \frac{\lambda}{\mu}$.
对于状态1: $p_0 \lambda + p_2 \mu = p_1\lambda + p_1 \mu$, 那么有: $p_2 = p_0 \frac{\lambda^2}{\mu^2}$.
…
对于状态n: $p_n = p_0 \frac{\lambda^n}{\mu^n}= p_0 \times \rho^n$, 这个就是一个等比数列.
由于$p_0 + p_1 + … p_n = 1$, 可以得到:
$p_0(1 + \rho + \rho^2 + … + \rho^n) = 1$.
根据等比数列的求和公式, 可以得到: $p_0 \times \frac{1 - \rho^n}{1 - \rho} = 1$, 其中$0 < \rho < 1$
由于在M/M/1 Queueing System中, 没有对顾客数量的限制, 当顾客数量$n \rightarrow \infin$时, 有:
$p_0 \times \frac{1}{1 - \rho} = 1$, 那么就得到了$p_0$的表达式:
由于$p_n = p_0 \times \rho ^ n$, 因此可以得到$p_n$的表达式为:
系统中平均顾客数
系统中的顾客数的平均值为: $N = \sum_{n=0}^{+\infin} np_n$.
将计算出的$p_n = \rho^n(1-\rho)$代入可以得到: $N = \sum_{n=0}^{+\infin}n\rho^n(1 - \rho)$.
进一步展开可以得到:
$N = \rho(1 - \rho) + 2\rho^2(1 - \rho) + 3\rho^3(1 - \rho) + …$
然后再展开:
$N = \rho - \rho^2 + 2\rho^2 - 2\rho^3 + 3\rho^3 - 3\rho^4 + …$
最后可以得到:
$N = \rho + \rho^2 + \rho^3 + … = \rho(1 + \rho + \rho^2 + …)$.
右侧当$n$趋于正无穷时, 收敛于$\frac{1}{1 - \rho}$, 因此可以得到M/M/1系统中顾客的平均数量为:
Queue中的平均顾客数
Queue中的平均顾客数也被称为排队长, 设排队长为$N_q$.
顾客在排队系统中的停留时间$T$由两部分组成:
- 在Queue中的等待时间$T_q$.
- Server的服务时间, 可以表示为$\frac{1}{\mu}$.
根据Little定理, $N_q = \lambda T_q$, $N = \lambda T$.
根据$T - T_q = \frac{1}{\mu}$, 可以得到:
$\frac{N - N_q}{\lambda} = \frac{1}{\mu}$.
那么可以得到$N_q$的表达式为:
因此, $N_q = N - \rho - \frac{\rho}{1 - \rho} - \rho = \frac{\rho^2}{1 - \rho}$
最终得到M/M/1 Queueing System的平均队长为:
顾客的平均停留时间
设$T$是这个顾客在排队系统中平均的停留时间.
根据Little定理, $T = \frac{N}{\lambda} = \frac{\rho}{1 - \rho} \times \frac{1}{\lambda} = \frac{1}{\lambda - \mu}$.
顾客的平均等待时间
设顾客在Queue中的平均等待时间是$T_q$, 那么根据Little定理, 有$T_q = \frac{N_q}{\lambda}$.
代入后得到: $T_q = \frac{\rho^2}{\lambda(1 - \rho)} = \frac{\lambda}{\mu(\mu - \lambda)}$
因此, 在M/M/1系统中, 顾客在Queue中的平均等待时间是:
其他指标
顾客到达后必须等待k个顾客以上的概率
现在要计算顾客到达后, 必须等待$k$个顾客以上的概率$P(n > k)$.
它的表达式是: $P(n > k) = \sum_{n = k + 1}^{\infin} p_n = 1 - \sum_{n=0}^kp_n$
将 $p_n = \rho^n (1 - \rho)$代入, 可以得到:
$P(n > k) = 1 - (1 - \rho + \rho - \rho^2 + \rho^2 - \rho^3 + … + \rho^k - \rho^{k+1}) = 1 - (1 - \rho^{k+1}) = \rho^{k+1}$
因此, $P(n > k) = \rho^{k+1}$.
顾客停留时间超过t的概率
$P(T > t) = e^{-(\mu - \lambda)t}$.
总结
对于M/M/1 Queueing System而言, 指标的计算公式如下:
| 指标 | 公式 |
|---|---|
| 系统中没有顾客的概率 | $p_0 = 1 - \rho$ |
| 系统中有n个顾客的概率 | $p_n = \rho^n(1 - \rho)$ |
| 排队系统中平均顾客数 | $N = \frac{\rho}{1 - \rho}$ |
| Queue中的平均顾客数 | $N_q = \frac{\rho^2}{1 - \rho}$ |
| 顾客平均停留时间 | $T =\frac{1}{\lambda - \mu}$ |
| 顾客平均等待时间 | $T_q = \frac{\lambda}{\mu(\mu - \lambda)}$ |
M/M/m Queueing System
M/M/m Queueing System和M/M/1的区别在于, Server的个数是m, 它的全称是M/M/m/∞/∞/FCFS
假设单位时间内, 每个Server的平均服务率是$\mu$, 那么Server整体的服务率就是$\bar{\mu}$可以表示为:
注意, 此时M/M/m Queueing System中, $\bar{\mu}$就和排队系统中的人数有关了, 在进行下面的推导时需要格外注意.
系统的繁忙度$\rho = \frac{\lambda}{m \mu}$, 只有当$\rho \in (0, 1)$时, 系统才会趋于稳定.
有$n$个顾客的概率
对于状态0来说: $\lambda p_0 = \mu p_1$, 也就是$p_1 = \frac{\lambda}{\mu} p_0$.
对于状态1来说: $\lambda p_0 + 2\mu p_2 = \mu p_1 + \lambda p_1$, 也就可以得到: $2\mu p_2 = \lambda p_1$, 因此, $p_2 = \frac{\lambda}{2\mu}p_1 = \frac{\lambda^2}{2\mu^2}p_0$.
对于状态2来说: 可以得到: $p_3 = \frac{\lambda}{3\mu}p_2 = \frac{\lambda^3}{6 \mu^3}p_0$.
因此, 最终$p_n$和$p_0$的关系可以表示为:
如果用系统的繁忙度来表示, 只需要将$\frac{\lambda}{\mu} = m \rho$代入即可, 得到的表达式为:
那么, 根据$\sum_{i=0}^{n}p_i = 1$, 将上面的表达式代入, 可以得到:
$\sum_{i=0}^{m-1}\frac{(m\rho)^i}{i!}p_0 + \sum_{i=m}^{n}\frac{m^m \rho^i}{m!}p_0 = 1$, 可以得到:
当$n \rightarrow +\infin$时, $\sum_{i=m}^{n} \rho^i$这一项会趋于一个定值, 因为$\rho \in (0, 1)$.
$\sum_{i=m}^{n}\rho^i = \sum_{i=0}^{n}\rho^i - \sum_{i=0}^{m-1}\rho^i = \frac{\rho^{m-1} - \rho^{n}}{1 - \rho}$, 当$n \rightarrow \infin$时, 这个定值是$\frac{\rho^{m}}{1 - \rho}$.
因此, 最终$p_0$的表达式就是:
那么最终$p_n$的表达式就是:
系统中人数多于m的概率
在M/M/m Queueing System中, 如果需要确定Server的个数$m$, 我们需要计算某几个指标.
首先, 一个指标是排队系统中人数多于$m$的概率是多少, 假设这个数值是$p_q$.
那么$p_q = \sum_{i = m}^{\infin}p_i = \sum_{i=m}^{\infin}\frac{m^m \rho^i}{m!}p_0 = \frac{(m\rho)^m}{m!(1-\rho)}p_0$.
此时, 如果将$p_0$的表达式代入, 就可以得到:
这个公式就叫做Erlang-C公式.
可以根据这个公式确定$m$的个数, 来让排队系统中多于$m$人的概率小于一个阈值.
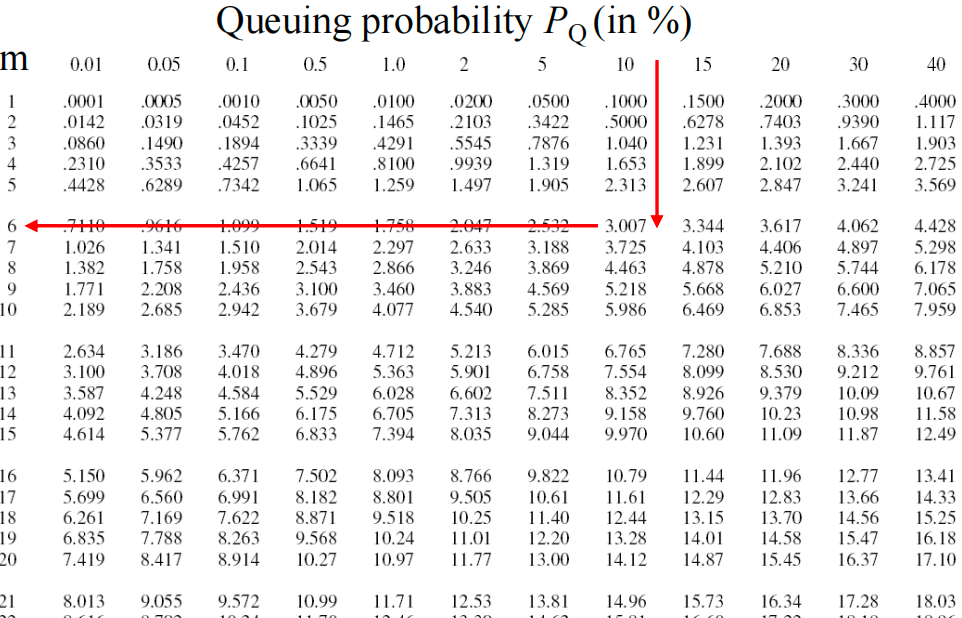
对于Erlang-C公式, 还存在一个Erlang-C表, 这个表的形式是:
- 行: 代表Server的数目$m$.
- 列: 代表$p_q$, 也就是系统中人数多于$m$的概率是多少, 这个概率以%为单位.
这个Erlang-C表格可以辅助确定$m$的数值, $m$的数值有如下两个约束:
- 排队系统的稳定条件: $\rho = \frac{\lambda}{m\mu} \in (0, 1)$, 这个可以求出$m > \frac{\lambda}{\mu}$.
- $p_q$的限制, 一般要求$p_q$小于一个概率.
因此, 有了这两个限制, 就可以在Erlang-C表格中, 先找到$p_q$的对应值, 然后向下找到第一个$m > \frac{\lambda}{\mu}$, 并且概率满足要求的最小的$m$, 就符合题意.
Queue中平均有多少个人(Server全部繁忙)
另外一个指标是, 假设现在$m$个Server都是繁忙状态, 那么我的Queue中平均有多少个人, 设这个值是$N_q$.
那么有: $N_q = \sum_{i=0}^{+\infin}ip_{i+m} = \sum_{i=0}^{+\infin}i \frac{m^m \rho^{i+m}}{m!}p_0 = \frac{(m\rho)^m}{m!}p_0\sum_{i=0}^{+\infin}i\rho^i$.
现在要计算$\sum_{i=0}^{+\infin} i\rho^i$, 这个无穷级数可以使用错位相减法, 最终的结果是$\frac{\rho}{(1-\rho)^2}$.
那么$N_q = \frac{(m\rho)^m}{m!}p_0 \frac{\rho}{(1-\rho)^2} = p_q \times \frac{\rho}{1 - \rho}$.
顾客的平均停留/等待时间(Server全部繁忙)
设m个Server全部繁忙的前提下, 顾客的平均等待时间是$T_q$, 那么根据Little定理:
- $T_q = \frac{N_q}{\lambda} = p_q \times \frac{\rho}{1 - \rho} \times \frac{1}{\lambda}$.
设顾客在排队系统中的平均停留时间是$T$, 那么$T$包括两个时间:
- 一个是平均等待时间.
- 一个是Server处理请求的时间, 这个时间就是$\frac{1}{\mu}$.
那么$T = T_q + \frac{1}{\mu} = p_q \times \frac{\rho}{1 - \rho} \times \frac{1}{\lambda} + \frac{1}{\mu}$.
M/M/m/m Queueing System
M/M/m/m Queueing System比M/M/m多了一个要求, 在排队系统中最多只能有$m$个顾客.
- 但是现在在排队系统中, 有$m$个Server, 因此, 还隐含着另外一个意思, 也就是说系统中是没有Queue的, 如果超过$m$个顾客来到了这个排队系统, 那么超过的部分就会直接离开.
有n个顾客的概率
在这种排队系统中, 只有$m+1$个状态, 状态转移图如下:
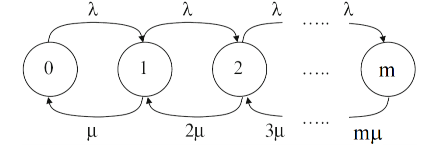
有Markov状态转移方程可以推导出: $p_n = \frac{\lambda^n}{n! \mu^n}p_0$.
将$\rho = \frac{\lambda}{m\mu}$代入, 可以得到:
又由于$\sum_{i=0}^{m}p_i = 1$, 代入可以求出:
系统被阻塞的概率
当M/M/m/m排队系统中$m$个Server全都被占满的时候, 整个系统就不再接受顾客了, 这种情况就是被阻塞了.
系统被阻塞的概率:
这个公式叫做Erlang-B公式, 同样, 也有一个Erlang-B表格.
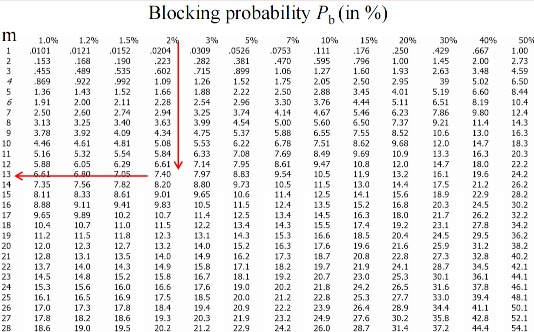
可以根据稳定条件$\frac{\lambda}{m\mu} \in (0, 1)$以及对阻塞概率$p_b$的要求找到最小的合适的Server数量$m$.
系统中的平均顾客数量
系统中的平均顾客数量可以表示为: $\bar{N} = \sum_{i=0}^mip_i = \sum_{i=0}^{m}i\frac{(m\rho)^i}{i!}p_0$.
将第一项删除, 可以得到: $\bar{N} = \sum_{i=1}^m i\frac{(m\rho)^i}{i!}p_0 = \sum_{i=1}^m\frac{(m\rho)^i}{(i-1)!}p_0 = m\rho\sum_{i=1}^m\frac{(m\rho)^{i-1}}{(i-1)!}p_0$.
然后再进行一次等价变形: $\bar{N} = m\rho\sum_{i=0}^{m-1}\frac{(m\rho)^i}{i!}p_0 = m\rho(1 - p_m)$.
因此, 在M/M/m/m系统中, 平均的顾客数量就是:
顾客的平均停留时间
由于M/M/m/m 会存在阻塞的情况, 因此需要计算真实进入这个系统的来客率, 假设这个来客率是$\lambda_{acc}$, 那么:
那么根据Little定理, 顾客的平均停留时间就是:
平均等待时间直接就是0, 因为根本没有队列.
M/M/∞ Queueing System
M/M/∞就是M/M/m 当Server的个数m趋于正无穷时候的情况.
有0个顾客的概率
对于这个系统, 状态有无穷多个, 状态转移图如下:
在M/M/m系统中, $p_0$的表达式为: $p_0 = (\sum_{i=0}^{m-1}\frac{(m\rho)^i}{i!})^{-1}$.
当$m \rightarrow \infin$时, $p_0 = \sum_{i=0}^{+\infin} \frac{(m\rho)^i}{i!} = e^{-m\rho}$.
根据麦克劳林级数: $e^x = \sum_{i=0}^{+\infin}\frac{x^i}{i!}$.
在M/M/m系统中, $p_n$和$p_0$的关系是: $p_n = \frac{(m\rho)^n}{n!}p_0$.
系统中顾客的平均值
系统中顾客的平均值$\bar{N} = \sum_{i=0}^\infin ip_i = \sum_{i=1}^{\infin}i\frac{(m\rho)^i}{i!}e^{-m\rho} = m\rho e^{-m\rho}\sum_{i=1}^{\infin}\frac{(m\rho)^{i-1}}{(i-1)!} = m\rho e^{-m\rho} \times e^{m\rho} = m\rho$.
因此, 在M/M/∞ 系统中:
顾客平均停留时间
根据Little定理, $T = \frac{\bar{N}}{\lambda} = \frac{m\rho}{\lambda} = \frac{1}{\mu}$.
由于是无限的Server, 因此, 平均等待时间是0, Queue的长度也是0.
排队系统的PASTA性质
PASTA的全称是Poisson Arrivals See Time Averages.
如果一个排队系统, 它的单位时间的到达人数服从参数是$\lambda > 0$的泊松分布, 那么这个排队系统就具有PASTA性质, 这个性质表述为:
- 一个人在任意$t$时刻来了, 看到前面有$n$个人的概率, 和这个系统本身有$n$个人的概率是一样的.
下面是PASTA性质的证明:
- $N(t)$: 这个排队系统在$t$时刻拥有的人数.
- $p_n(t)$: 这个排队系统在$t$时刻有$n$个人的概率.
- $A(a, b)$: 一个事件, 表示一个人在时间段$[a, b]$内到达排队系统.
那么, 一个人在$t$时刻来了, 看到前面有$n$个人的概率就可以被表示成: $\lim\limits_{\Delta t \rightarrow 0}\{N(t) = n \ |\ A(t, t + \Delta t)\}$.
根据贝叶斯公式:
由于泊松分布的性质, $P\{A(t, t + \Delta t) \ |\ N(t) = n\} = P\{A(t, t + \Delta t)\}$.
因此, 右侧就等于$\lim\limits_{\Delta t \rightarrow 0 }P\{N(t) = n\} = p_n$, 也就证明完毕.
M/G/1 Queueing System
M/G/1 Queueing System和M/M/1的区别在于, Server处理顾客的分布不再是泊松分布, 而可能是任意分布.
- 那么, 就不能再用Markov排队系统去求解$p_n$.
顾客平均等待时间
假设在M/G/1 Queueing System中:
- $x_i$: Server处理第$i$个到来的顾客需要的时间, 它们的期望$E(x_i) = x = \frac{1}{\mu}$.
- $N_i$: 当第$i$个顾客到来的时候, 它发现队列中有多少个人.
- $R_i$: 当第$i$个顾客到来的时候, 它可能会发现Server在忙, 那么Server忙多久可以处理下一个顾客, 这个$R_i$就是这个时间, 叫做residual service time.
那么假设第$i$个顾客的等待时间是$T_q(i)$, 那么:
然后让两边同时取期望, 就得到: $E[T_q(i)] = E(R_i) + E[\sum_{j=i - N_i}^{i-1}x_j]$.
由于$x_i$和$N_i$独立, 因此: $E[T_q(i)] = E(R_i) + E[\sum_{j=i - N_i}^{i-1}x_j] = E(R_i) + E(x)E(N_i) = E(R_i) + \frac{1}{\mu}E(N_i)$.
设$R$是平均的residual time, 那么$R = \lim\limits_{i \rightarrow +\infin} E(R_i)$.
将等式两边同时取$i \rightarrow +\infin$的极限, 可以得到: $T_q = R + \frac{1}{\mu} N_q$, 其中$T_q, R, N_q, \mu$都是平均值.
又根据Little定理, $N_q = \lambda T_q$, 可以得到$T_q = R + \rho T_q$, 因此M/G/1系统的平均等待时间就是:
之后, 需要计算所有顾客residual service time的平均值, $R_i$随时间的变化图如下:
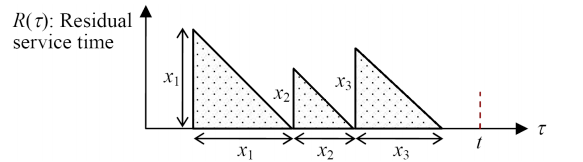
取一个时间段$[0, t]$, 那么$R(t) = \frac{1}{t} \int_{0}^{t}R(\tau)d\tau$, 这个积分本质上就是求若干个三角形的面积之和.
那么$R(t) = \frac{1}{t}\sum_{i=1}^{M(t)} \frac{1}{2}x_i^2$, 其中$M(t)$表示时刻$t$前面有几个这样完整的等腰直角三角形, 因为后面要取$t \rightarrow \infin$的极限, 所以不考虑细节.
然后做一次等价变形: $R(t) = \frac{1}{2} \frac{M(t)}{t} \frac{\sum_{i=1}^{M(t)}x_i^2}{M(t)} $.
然后, 等式两边取$t \rightarrow \infin$的极限:
- 观察$\frac{M(t)}{t}$, 这个本质上是顾客到达的平均速率(一个顾客就是一个等腰三角形), 当$t$趋于正无穷时, 这个值就趋近于$\lambda$.
因此, 可以得到平均的residual time是:
由此, 可以得到最终的顾客平均等待时间是:
这个公式叫做Pollaczek-Khinchine formula, 简称PK公式.
根据期望的性质, $E[x^2] = D[x] + (E[x])^2$, 因此只要知道了$E(x)$以及$D(x)$, 就可以知道$E[x^2]$.
Queue中的平均顾客数
根据Little定理, Queue中的平均顾客数: $N_q = \lambda T_q = \frac{\lambda^2 E[x^2]}{2(1 - \rho)}$
顾客平均停留时间
$T = T_q + x = \frac{\lambda E[x^2]}{2(1 - \rho)} + \frac{1}{\mu}$.
系统中顾客平均数
根据Little定理, $N = \lambda T = \frac{\lambda^2 E[x^2]}{2(1 - \rho)} + \rho$.
一种特殊情况: M/D/1
D表示Server的处理速率是一个常数, 那么$E[x^2] = (E[x])^2 = \frac{1}{\mu^2}$.
代入PK公式, 可以得到: $T_q = \frac{\rho}{2\mu(1 - \rho)}$.
对于M/M/1系统来说, $T_q = \frac{\rho}{\mu(1-\rho)}$, 这个值是明显大于M/D/1的.
因此, M/D/1系统比M/M/1系统的平均等待时间更短.
带优先级的M/G/1 Queueing System
之前讨论的M/G/1 Queueing System的服务方式是FCFS, 现在的服务方式是以优先级为基础的, 需要做出如下调整:
- 假设优先级分为$n$个级别, 越小表示有越高的优先级, $1, 2, 3, …, n$.
- 现在有$n$个平行的Queue, 分别存储对应优先级的顾客, 例如优先级是1的顾客到编号是1的Queue.
- 如果Server空了, 高优先级的队列中的顾客先来.
如果考虑优先级, 那么系统又可以分为抢占式和非抢占式:
- 非抢占式: 如果低优先级顾客的正在服务, 这个时候来了一个高优先级的, 那么等低优先级的服务完, 高优先级的再上.
- 抢占式: 高优先级的来了之后直接抢占Server, 等所有高优先级的服务完了, 低优先级的再服务.
非抢占式的M/G/1 Queueing System
假设有下列notation:
- $\lambda_k$: 优先级为$k$的顾客的平均到达率.
- $\mu_k$: 优先级为$k$的顾客的平均离开率.
- $N_{q,k}$: 优先级为$k$的顾客的queue中的平均顾客数.
- $T_{q, k}$: 优先级为$k$的顾客在queue中的平均等待时间.
- $\rho_k$: 对于优先级为$k$的顾客的Server的繁忙度.
- $R$: 对于所有顾客平均的residual time.
对于这个Queueing System, 它能够趋于稳定的条件是: $\rho = \sum_{i=1}^n \rho_i < 1$.
平均的Residual Time
假设:
- $x_{i,j}$表示Server处理优先级是$j$的第$i$个顾客所用的时间.
- $M_j(t)$: 表示$[0, t]$时间段内, 优先级是$j$的顾客来了几个.
那么, 在$[0, t]$时间内, 所有顾客的平均Residual Time就可以表示成:
当$t \rightarrow +\infin$时, $\frac{M_j(t)}{t}$本质上就是优先级为$j$的顾客的来客率, 可以表示为$\lambda_j$, $\frac{1}{M_j(t)}\sum_{i=1}^{M_j(t)}x_{i,j}^2$本质上就是优先级为$j$的顾客, $x_j^2$的期望值, 也就是$E[x_j^2]$.
因此, 最终的Residual Time可以表示为:
优先级为k的顾客平均等待时间
对于优先级是1的顾客, 根据PK公式: $T_{q, 1} = R + \frac{1}{\mu_1}N_{q, 1}$.
根据Little定理, $N_{q, 1} = \lambda T_{q, 1}$, 可以求出: $T_{q, 1} = \frac{R}{1 - \rho_1}$.
对于优先级是2的顾客: $T_{q, 2} = R + \frac{1}{\mu_1} N_{q, 1} + \frac{1}{\mu_2} N_{q, 2} + \frac{1}{\mu_1} \lambda_1 T_{q, 2}$, 这个公式包含三个部分:
- 处理优先级是1的顾客.
- 处理优先级是2的顾客.
- 处理一个优先级是2的顾客时, 优先级为1的顾客可能来了, 那么处理完这个优先级是2的顾客后, 又需要处理这部分多余的顾客, 这个过程会交替进行.
然后, 将Little定理: $N_{q, k} = \lambda_k T_{q, k}$代入上面的式子, 可以得到:
$T_{q, 2} = R + \rho_1 T_{q, 1} + \rho_2 T_{q, 2} + \rho_1 T_{q, 2}$.
可以求出: $T_{q, 2} = \frac{R + \rho_1 T_{q, 1}}{(1 - \rho_1 - \rho_2)}$, 之后, 将$T_{q, 1} = \frac{R}{1 - \rho_1}$代入, 可以得到$T_{q, 2} = \frac{R}{(1 - \rho_1)(1 - \rho_1 - \rho_2)}$
根据这个形式, 可以得到更通用的格式:
抢占式的M/G/1 Queueing System
排队网络
上面阐述的排队系统, 基本上就是若干个Queue, 和若干个Server组成的一个排队系统, 但是在真实的网络环境下, 一般都是好几个排队系统连接在一起, 成为排队网络.
排队网络可以分成如下几类:
- Closed Queueing Network: 在这种排队网络中, 不会有新的顾客进来, 不会有顾客离开, 里面的顾客就在这个排队网络中兜兜转转.
- Open Queueing Network: 有新的顾客进来, 也有新的顾客离开.
- Feed-Forward Network: 在这种排队网络中, 不会出现从一个排队系统中出来的顾客又跑回原来进去过的排队系统中, 也就是说排队系统之间的连接只有前向边, 没有反向边.
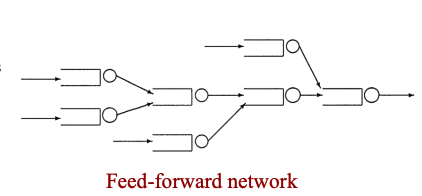
串联排队网络分析
假设两个排队系统串联起来, 示意图如下:
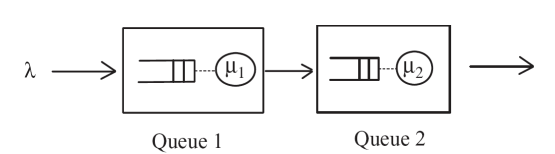
对于排队系统1来说, 它是一个M/M/1排队系统, 来客率是$\lambda$, Server的处理速率是$\mu_1$.
对于排队系统2来说, 它的Server处理速率是$\mu_2$.
现在的问题是, 对于排队系统2来说, 它的来客率是怎么分布的?
假设顾客A从Queue 1中离开, 这个时候需要分两种情况:
- 情况1: A走了之后, Queue1变成空的了, 这个时候, 从A到达Queue2, 到下一个顾客到达Queue2的时间间隔可以分成两个部分:
- 下一个顾客到达Queue1.
- 下一个顾客在Queue1中被处理完.
- 情况2: A走了之后, Queue1还没有空, 那么这个时候, 从A到达Queue2, 到下一个顾客到达Queue2的时间间隔就是下一个顾客在Queue1中被处理的时间.
由于Queue1变成空的概率$p_0 = 1 - \rho$, 两个顾客到达Queue2的间隔时间是$f$, 那么:
其中, $f_{empty}$是两个参数分别为$\lambda$和$\mu_1$的指数分布的和, 是一种超指数分布, 分布密度函数是: $f_{empty} = \frac{\mu_1\lambda}{\mu_1 - \lambda}(e^{-\lambda t} - e^{-\mu_1 t})$.
$f_{busy} = \mu_1e^{-\mu_1t}$.
那么最后:
因此, 对于Queue2来说, 它的来客率也是$\lambda$.
Burke定理
Burke定理有两条内容:
- 对于M/M/-这种排队系统, 从这个排队系统吐出来的顾客的速率和来客率一样, 都是$\lambda$.
- 对于M/M/-这种排队系统, 假设有$n$个串联起来, 那么:
- 排队系统i有
x个人, 排队系统j有y个人, 排队系统k有z个人的概率是独立的, 也就是说: $P\{N(i)=x, N(j)=y, N(k)=z\} = P\{N(i)=x\} \times P\{N(j)=y\} \times P\{N(k)=z\}$
- 排队系统i有
Kleinrock独立性估计
Kleinrock有如下几个假设:
一个排队网络中, 顾客到达所有排队系统的速率都服从指数分布.
对于一个排队网络, 每个排队系统的Server处理时间之间是独立的, 并且处理时间服从指数分布.
- 这是一个合理的假设, 因为Server的处理时间一般来说是和packet的长度有关, 但是packet的长度是固定的.
如果有这些假设, 那么排队网络的端到端延时就可以估计, 公式为:
其中, $\mu_i, \lambda_i$就是这个顾客走过的所有排队系统的来客率和对应Server的处理速率.